The Problem

 If you are living in a democratic society, you are likely accustomed to the “one person one vote system” that fuels most of the decision-making in modern governments. “One person one vote” means exactly as it sounds, each person gets to cast a single vote for their first choice on a ballot. This system is what we’re familiar with, and you may have never even questioned it. There are a few major problems with this system that have been plaguing society for centuries. This article will attempt to cast a light on these issues and discuss an innovative voting mechanism that aims to alleviate some of democracy's greatest challenges.

Problem 1: Tyranny of the Majority

Tyranny of The Majority in Ancient Greece

 Western democracy is rooted in fifth century B.C. Athens. The Athenian system allowed each man who was a citizen of Athens to cast a vote on pressing issues. The policy that achieved a majority of the votes would be passed. It was at this moment that one person one vote, along with majority rule became the default consensus mechanism for western democracy. The greeks quickly realized that all the political power had been given to the “mob”. The greeks called this an ochlocracy and described it as one of the three bad forms of government (along with tyranny and oligarchy) due to its tendency to infringe on the rights of minorities. In one famous incident that occurred during the Peloponnesian War, the assembly condemned a group of generals to death after they failed to rescue a group of survivors from a nearby island. Later, the assembly was convinced that a storm had prevented the generals from acting and condemned their accusers to death. Growing more and more concerned about mob rule, the Athenians devised a more modest form of democracy that gave more influence to governing bodies including a commission that could propose legislation. The members of these bodies were selected by the assembly, and so began the long history of trying to manage majority rule.

America’s Contribution to Mob Rule

 Fast forward to the birth of American democracy, where the founding fathers were very concerned over the majority’s ability to ignore the rights of the minority. Their solution: divide the national government into three branches to place “checks and balances” on each other, and limit the voting power of the majority by placing the final decisions on the president and senators with state legislatures. They also required various degrees of super majority consensus to be achieved to pass major decisions. They were also aware of the opposite problem, gridlock. Before the constitution was written, gridlock was a more prominent problem. In order to achieve anything of note, the national government could only act with the support of the states and most of these actions required a super majority or unanimous consensus. However, a super majority or unanimous voting scheme is susceptible to hold out from unreasonable groups who know that action cannot be taken without their support. Aware that gridlock could paralyze a democracy while also being concerned with the rights of minorities, the framers of the U.S constitution settled on a compromise between the tyranny of the majority and gridlock. This system endured passably, but ethnic and religious minorities continued to suffer at the hands of a conservative majority. In the second half of the 20th century, the federal courts stepped in to fix the problem by recognizing the rights of minority groups to equal political representation, education, and other resources. At the same time, congress passed civil rights laws to protect the freedoms of all citizens, including those previously neglected. Readers are well aware of the tribulations that have come after this movement but despite that, this was one of America's greatest contributions to the problem of majority rule. These political and legal concepts are often taken as assumptions, however, it took over two thousand five hundred years since the conception of democracy to get where we are today. And, although immense progress has been made to combat the flaws of majority rule, we still suffer from the fundamental flaws of this system.

Problem 2: Condorcet Voting Paradox

 Nicolas de Condorcet was an 18th-century philosopher and mathematician who pioneered the mathematical study of voting. Condorcet is famous for his jury theorem and the “Condorcet paradox”. This paradox is perhaps best explained with an example. Suppose Ali, Helen and Nick need to vote on where to direct taxpayer funds. The options they can vote on are: to build more bike paths in the city, improve the existing subway system or build a new road connecting major city centres. Each member proceeds to rank their choice from first to last. Ali being an avid cyclist votes bike path, subway, road (in order of preference). Nick loves his new car so he votes road, bike path, subway. Finally, Helen lives in the city and would benefit greatly from an improved subway so she votes, subway, road, bike.

Polcity	Ali	Helen	Nick
Improve Bike Path	1	3	2
Improve Subway	2	1	3
Build Road	3	2	1

 If we analyze the choice between improving the bike path and improving the subway, the bike path would prevail 2-1 since Ali and Nick both prefer the bike path to the subway. If we then compare the choice between the subway to the road, the subway prevails 2-1 as Ali and Helen both prefer the subway to the road. Finally, when the voters chose between improving the bike path and building the road, the road would prevail 2-1 as both Helen and Nick preferred the road to the bike path. In aggregate there is no determinate outcome; the bike path beats the subway, the subway beats the road but the road beats the bike path. The problem is that in this system, a vote only tells you if someone prefers one option over the other but not how much they prefer it. Building off the work of the Marquis de Condorcet, Kenneth Arrow formalized this paradox into a political theorem known as the “Impossibility Theorem”. Arrow’s impossibility theorem formally proves that any voting system in which individuals rank candidates could never overcome issues of this nature.

Problem 3: Strategic voting

 Strategic voting has been on the rise in western democracies. Strategic voting (or tactical voting) refers to when an individual does not vote for who they align with most politically. Instead, they vote for the lesser of two evils in an effort to “make their vote count”. Every election cycle more and more digital tools get released that help voters predict the most “effective” vote to cast. Here is an example for the Canadian elections. In the previous 2020 election, president Joe Biden heavily promoted himself as the only one who could defeat incumbent Donald Trump. The most sinister example of strategic voting however was the rise of the Nazi party. In his book The Coming of the Third Reich, historian Richard Evans observes that no more than 10% of the German public were ever strong supporters of the extreme right. However, in the 1930 election, Hitler won an additional 10% of the votes from people who cast strategic votes against a political system they deemed to be corrupt and unresponsive to their needs. In the following election, many middle-class germans voted for the Nazis as their only chance to prevent Stalinist Red Terror from spreading throughout Germany, allowing Hitler to become the chancellor. At the same time, the minority groups, particularly Jewish people felt threatened by Hitler and were pushed further to the edges of the political spectrum, casting strategic votes for the communist party of Germany, reinforcing the middle-class view that if Hitler lost, communism would win. This downward spiral ushered in Nazi dictatorship the following year. Strategic voting seems to be inevitable in first-past-the-post systems (the candidate with the most votes wins, and the losing candidates get no representation). It is easy to see from this example how this aspect of democracy can be abused by savvy leaders to achieve power all while pitting factions of society against themselves. Even less extreme, strategic voting results in individuals voting for policies or candidates they do not believe in which flies in the face of what true democracy should be.

 Modern democracy based on majority rule has surely proven to be a positive invention for humanity and has led to greater equality over the last century, but it is not without its faults. From its inception, it has struggled to balance the needs of the majority while protecting the rights of the minority. Its tendency to encourage strategic voting has repeatedly been abused to establish dictatorships and has led to paradoxical victories. All of these issues stem from the inability of our democracy to convey the intensity of people's interests, needs, and the superior expertise of particularly knowledgeable voters.

Solution: Quadratic Voting

What is Quadratic Voting

 Quadratic Voting (QV) is a redesigned voting system that aims to alleviate the issues plaguing the current “one person one vote” system by allowing individuals to express not just what option they would prefer, but how much they would prefer it.

How Does Quadratic Voting Work?

 To allow for the intensity of opinions to be expressed, each voter is given a budget of “voice credits” that they can allocate amongst a variety of issues on a ballot. These credits convert to “counted votes” based on the square root of the voice credits cast on that issue. In simple terms, the first vote will cost you one voice credit (because 1^2 =1), the second vote costs four (because 2^2=4), the third costs nine (because 3^2=9) etc. QV implies that individuals are able to cast multiple votes for issues they feel strongly about, but each vote will cost them more than the previous one. The quadratic nature of this system means that it is more efficient (in terms of spending your voice credits) to spread your votes across a variety of issues. The result is that once all credits are spent, the output should reflect how strongly the population desires certain outcomes.

The formula for the cost of a vote is as follows:

number of voice credits needed = (number of votes)²

Number of votes	Cost In Voice Credits
1	1
2	4
3	9
…	…
10	100

Why

 The current system essentially decomposes each vote into one of the three levels of preference: yes, no, and indifferent. Enabling individuals to signal the strength of their preferences unlocks two key properties.

• A passionate minority can outvote an indifferent majority
•  solving the problem of the tyranny of the majority
• The outcome should maximize the well-being of the entire group
•  eliminating Condorcet’s voting paradox

Why Quadratic?

 Politics is largely concerned with creating and managing goods and services that affect the entire population. The economic term for this is public goods. Examples of public goods are transit systems, universal healthcare, and scientific research. In contrast, private goods are goods that are consumed by individuals or a subset of the population. An example of a private good is the banana you purchased at the store or your house. The mechanism used to allocate private goods is the market (or at least typically), where goods are bought and sold for a price. A standard market is designed to allocate a private good to the individual who values it the most. The allocation of public goods is fundamentally different than private goods in that instead of allocating it to the person who values it the most, public goods must be allocated in the way that maximizes the overall well-being of the entire population. Naturally then, to do this effectively, we would want each citizen’s voice to be heard in proportion to how important a good is to them. If we were to adopt a traditional market mechanism to allocate public goods, we would replace the tyranny of the majority with the tyranny of the richest (we also see this in some aspects of society). William Vickrey, a Nobel prize-winning economist made a key insight. In an auction, “each individual must pay an amount equal to the cost that their actions impose on others”. When you buy corn at the grocery store, you are paying the price for that corn to not be used in the second best way, and therefore are compensating society for what it gives up by allocating the corn to you. In voting, you should have to pay for the harm imposed on people by outvoting them. Therefore the amount you pay must equal the amount your vote denies others the value they would receive from a different outcome. Okay, but why quadratic? In their 1976 paper, Optimal Allocation of Public Goods: A Solution to the “Free Rider” problem, economists Theodore Groves and John Ledyard proposed that the price individuals should pay for influencing public goods should be proportional to the square of their influence. To understand this let's first look at an example where the cost of votes scaled linearly (1 vote costs 1 voice credit, 10 votes costs 10 voice credits). Imagine an individual who has a disproportionately strong preference on an issue relative to the population, call this person A. In contrast, imagine an individual has a much weaker preference about this topic but generally cares about a variety of policies. We will call this person B. In this situation, person A can easily influence the outcome of their preferred policy and pay relatively little. Person B is likely to cast none or very few votes on that policy as they are giving up overall influence for an issue they do not feel strongly about. The problem is that votes are too cheap for people that care most about an issue but too expensive for those who care a little. The solution…? to make the next vote more expensive for those who have already cast votes on a policy than it is for people who are casting their first vote. This encourages people who care a little to at least buy a few votes and discourages people who care a lot from buying too many. If the cost of casting more votes increased too steeply, passionate voters would vote too little for an issue and we would fall closer towards a tyranny of the majority. If it cost less, those with strong preferences would have too much influence.

• source: Quadratic Payments: A Primer - Vitalik Buterin's website

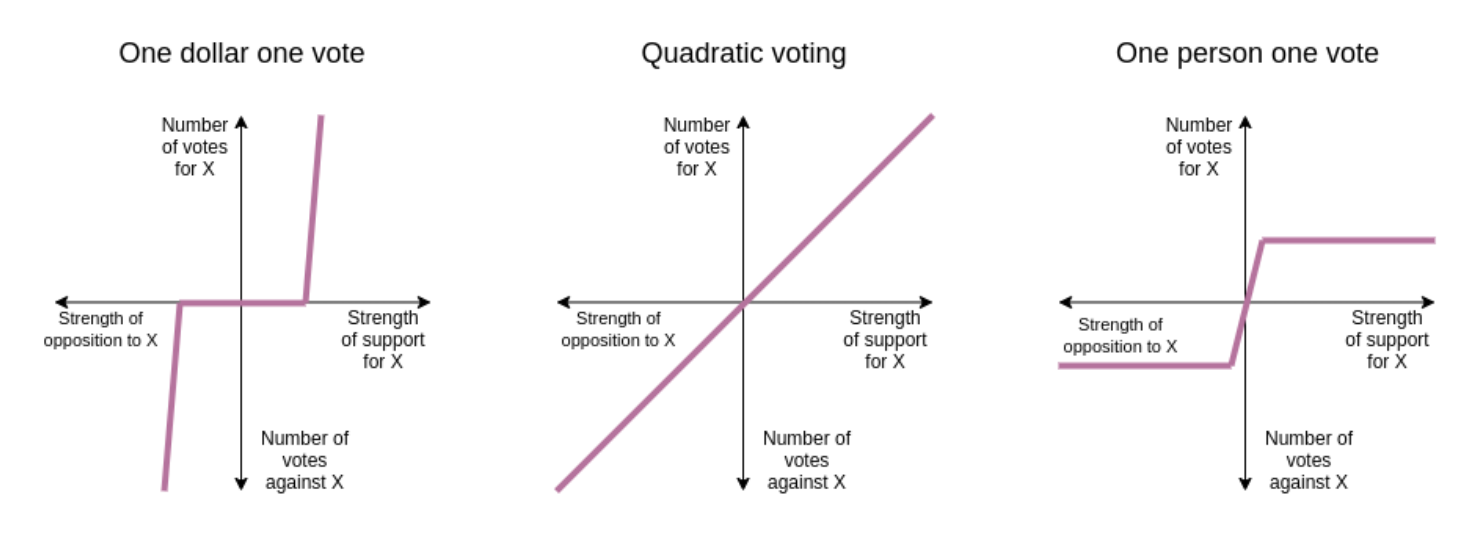
 QV enables individuals with strong preferences to influence the outcome of an election in direct proportion to the strength of their preferences. When the intensity of everyone's preferences are similar, the majority will prevail. However, when the minority has sufficiently intense preferences or reaches sufficient size, they will be able to protect their interests from the majority. QV addresses Condorcet’s voting paradox by giving weight to both the numbers and the intensity of interests, and therefore can approximately optimize the aggregate well-being of society.

How Can Quadratic Voting Be Applied Today?

 In being such a radical shift in how we collectively make decisions, it would not be wise to replace our current system with quadratic voting overnight. Instead, let’s explore some of the potential low-hanging fruit that could be harvested from quadratic voting.

 The most common survey method today is the Likert survey. In a Likert survey, participants are asked for their opinion on a scale from “strongly disagree” to “strongly agree”. Most people who have participated in polls are familiar with the Likert scale. The problem with this scale is its tendency to force participants to extremes. Due to its oversimplification of opinions, those who care at all about an issue are more likely to vote for one of the strong preferences when in reality they lie closer to the centre. The result is a characteristic “W” shape in the distribution of opinions.

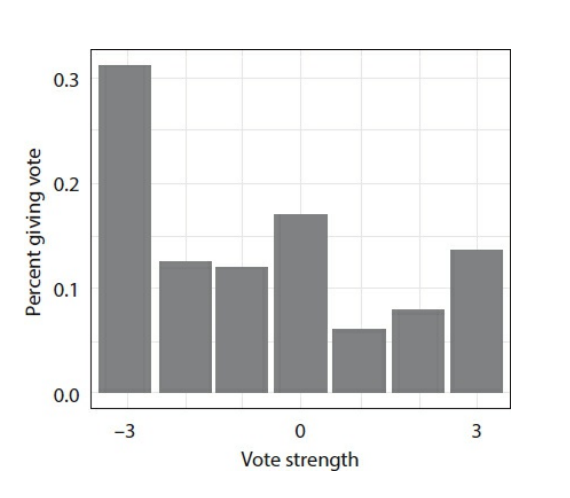
• Frequency of participants’ expression positions ranging from strong disagreement to strong agreement with a national ban on abortion in the United States. Source: Adapted from David Quarfoot, Douglas von Kohorn, Kevin Slavin, Rory Sutherland, David Goldstein, & Ellen Konar, Quadratic Voting in the Wild: Real People, Real Votes, 172 Pub. Choice 283 (2017), p. 6.

 Most people would agree that this distribution is counterintuitive and the real distribution of opinions should more closely resemble a bell curve. Since quadratic voting is specifically designed to signal the strengths of preferences, it seems natural that a good testing ground for QV would be in polling. In 2016 David Quarfoot and colleagues ran a study in which participants took a survey on whether or not to appeal Obamacare. Some groups used the standard Likert scale, some groups used quadratic voting, and some used both, but the content of the survey was identical. The results are pictured below.

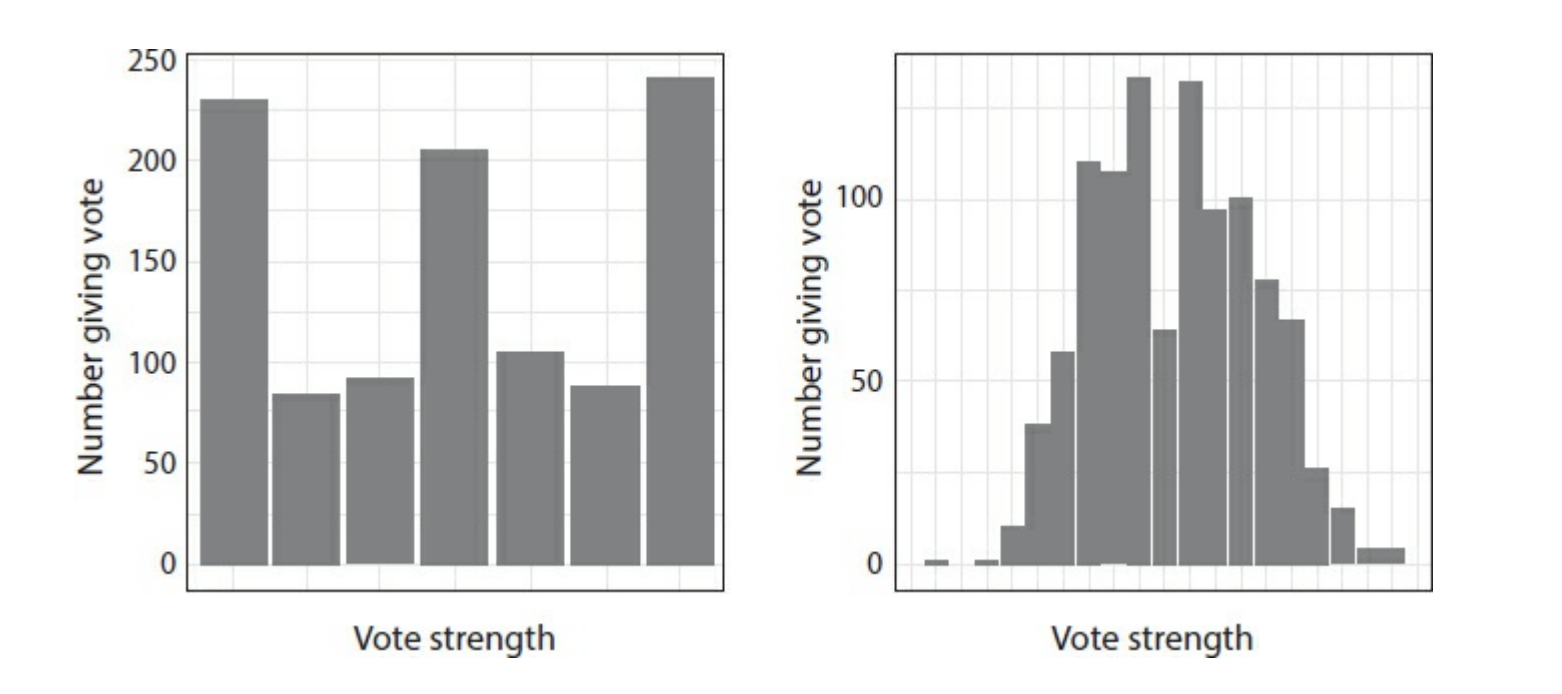
• Survey results for appealing Obamacare. Source: David Quarfoot, Douglas von Kohorn, Kevin Slavin, Rory Sutherland, David Goldstein, & Ellen Konar, Quadratic Voting in the Wild: Real People, Real Votes, 172 Public Choice 283 (2017).

 The QV poll resulted in bell-like distribution whereas the Likert scale produces its signature “W ” shaped distribution. More important, is the added nuance in the QV poll results. The results demonstrate that most people lie closer to the centre when it comes to repealing Obamacare but the Likert results suggest the opposite.

 Another interesting discovery in Quartfoot’s poll was that a participant's willingness to sign up for emails about a particular issue was directly correlated to the strength of their preferences revealed in the QV poll. The same could not be said for the Likert survey. This data suggests that QV might be a valuable tool in not only gaining better insights into people's preferences but also as a way for survey designers to curate their audience.

How Can Quadratic Voting Be Applied In The Future?

 Quadratic voting has the potential to dramatically improve our current political elections. By allowing those with significantly strong opinions to be heard, quadratic voting can solve the tyranny of the majority problem. But what can quadratic voting do to help us alleviate the pitfalls of strategic voting? In the book Radical Markets (from which most of the ideas in this article come from), authors Glen Weyl and Eric Posner propose a potential solution. Quadratic voting could get applied at the candidate nomination level (when parties pick their leaders). Voters could cast as many votes as they wish in favour or against any candidate. Due to the quadratic nature of the system, it is more efficient to divide one's votes for a favoured candidate as well as against their opponents, as opposed to just in favour (or just against). Strategic voting occurs when voters feel that voting for their preferred candidate would be a waste of a vote (since that candidate might be obscure or their constituency might have strong ties to a party) and so they end up voting for the lesser of two evils. In this revised system, there would be no point in casting a vote in favour of the “lesser of the two evils candidate” when they could just cast a vote against the “most evil” candidate for the same cost in voice credits. In the end, candidates that receive positive overall votes must be more highly regarded than the rest. Using quadratic voting for choosing political candidates would effectively eliminate strategic voting, giving more of a chance to “smaller” candidates and diminishing the role of extremist views in politics.

• Source: The Economist has provided a visual playground for this sort of voting scheme.

Real-World Examples

Colorado

 In April 2019, the democratic caucus of the Colorado State House of Representatives used quadratic voting to vote on over 100 proposed bills. This came after weeks of discussion with no action. The results showed a general approval of the Equal Pay for Equal Work Act which was passed a few months later. No member of the caucus used all of their credits on a single bill, strengthening quadratic voting's case for being an improved voting design. This marks the first major use case of quadratic voting in politics.

Read more

Taiwan

 In 2019, Taiwan conducted their annual Presidential Hackathon in which quadratic voting was used to choose the winning projects.